非接触几何测量中的误差解耦算力与高信噪比感知硬件的深度融合

更新时间：2025-12-23

点击次数：26

摘要 (Abstract)

在任何精密制造（Precision Manufacturing）领域，大尺寸工件内径、圆度的现地测量（In-situ Measurement）始终是攻克生产效率瓶躯的关键。随着工业4.0的演进，基于激光位移传感器的非接触式测量方案逐渐在传统的固定式CMM（三坐标测量机）与以及纯手工量规之间，找到了一条兼具精度与效率的新路径。然而，非接触测量系统在带来无损检测优势的同时，也引入了全新的挑战——系统几何安装误差以及传感器本身的光电信号置信度问题。本文将深入剖析经典的“三点法"模型中的角度维安装误差传播机制，提出基于广义逆矩阵的自校准数学模型，并论证该模型对传感硬件（特别是激光三角位移传感器探头）在光学抗噪设频、非线性误差控制及数据传输层面的苛刻要求，以国内超高精度厂商泓川科技（Chuantec）的LTP系列传感数据为锚点，探讨软硬件协同下的微米级系统构建法则。

第1章：非接触测量基础：三点法几何建模的内生优势

在航空航天舱体内衬、重反舰曲轴孔以及高能物理实验装置的筒体检测中，被测对象往往具有难以移动、直径尺度大、表面反射特性复杂等特点。经典的空间三坐标测量或影像测量仪受制于量程与接触力影响，往往无法实施100%全检。

相对静止或做回转运动的激光测头组便成了最you解。基于经典的欧几里得几何，当已知圆上三个坐标点 $P_{1}, P_{2}, P_{3}$ 时，即可唯yi确定该圆的半径 $R$ 和圆心 $O (x_{0}, y_{0})$ 。

这从理论上不仅优雅而且鲁棒性ji高：
构建坐标系 $X O Y$ ，设测头理论安装光轴呈120°分布，各传感器探头中心到理论几何中心O对于距离为 $l_{1}, l_{2}, l_{3}$ ，传感器实际测得的位移读数为 $m_{1}, m_{2}, m_{3}$ 。

理论模型下，传感器探点 $N_{i} (i = 1, 2, 3)$ 的物理坐标可以清晰地表述为距离常量 $l$ 与位移变量 $m$ 的线性叠加。对于理想圆，半径方程可联立如下：

${\begin{cases} R^{2} = (x_{p} - (l_{1} + m_{1}))^{2} + y_{p}^{2} \\ \dots \end{cases}$

然而，这仅仅是处于“真空"中的理想情况。一旦引入工业现场复杂的震动环境与装夹公差，真正的工程噩梦才开始。

第二章：误差传播的隐形杀手——角度安装偏差建模

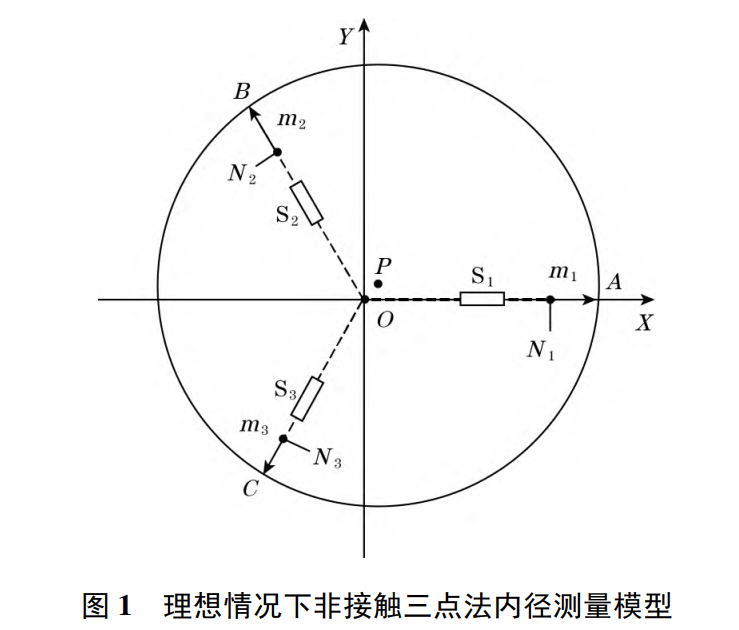
钟亦林等人在上海交通大学的研究中详细指出了仅仅修正线位移误差 $(x_{p}, y_{p})$ 的局限性。在实际工程，传感器在径向方向安装时，受限于夹具加工精度与微量调节机构的操作限制，不可避免地会产生安装偏离角度。

我们不仅仅有圆心偏移，还存在探头光轴相对于理论径向的偏角——我们称之为角度安装误差 (Angle Setting Error) $α_{i}$ 。

即使极其微小的 $α$ 角（例如： ${0.1}^{\circ}$ ~ $1^{\circ}$ ），在测量大直径（例如 $Φ > 500 m m$ ）工件时，根据正弦放大效应，也会造成百微米级的系统性测量偏差（Systematic Bias），且这个偏差是一个高度非线性的耦合项。

传统的做法是采用高精度的标准规（System Master）进行标定。但在大型现场，制造一个直径1000mm且圆度误差小于0.5µm的标准圆规，其成本是天文数字，且不易保存。因此，探索算法层面的无标准规自校准（Calibration without Artefact knowledge）成为学界的金杯。

修正后的数学模型变为关于 $α_{i}$ 的显函数：

$O N_{i} \frac{(l_{i} + m_{i}) \cos (y_{i} - α_{i}) \pm \sqrt{r^{2} - (l_{1} + m_{1})^{2} \sin^{2} (y_{i} - α_{i})}}{\cos γ_{i}}$

上式不仅引入了探头到被测壁面距离的三级关联，甚至要求对二阶微小量进行解算。经过钟亦林教授等多点实验论证，通过旋转被测目标，获得至少 $n \geq 4$ 个不同位置的数据组，并利用广义逆矩阵与Newton-Raphson迭代求解法，可以在不知道对标真值的情况下收敛出每一支传感器的原始偏转角 $α_{i}$ 。

第三章：传感器的关键性：一切精密测量的物理基石

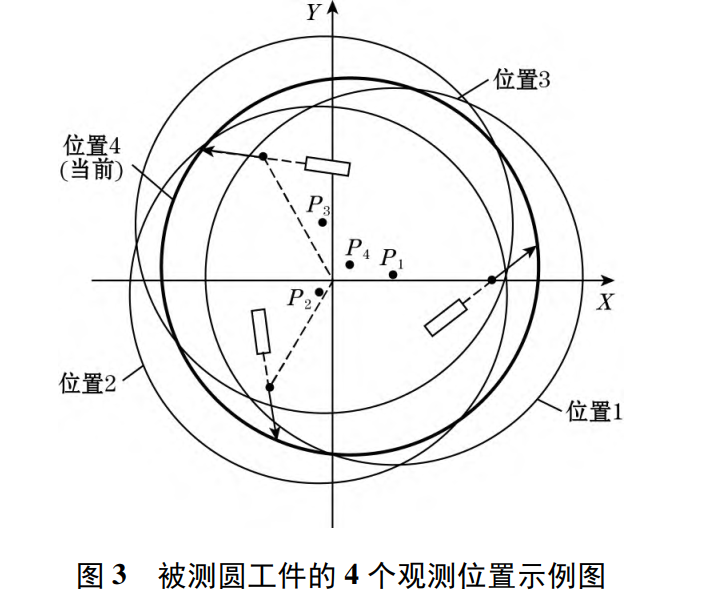
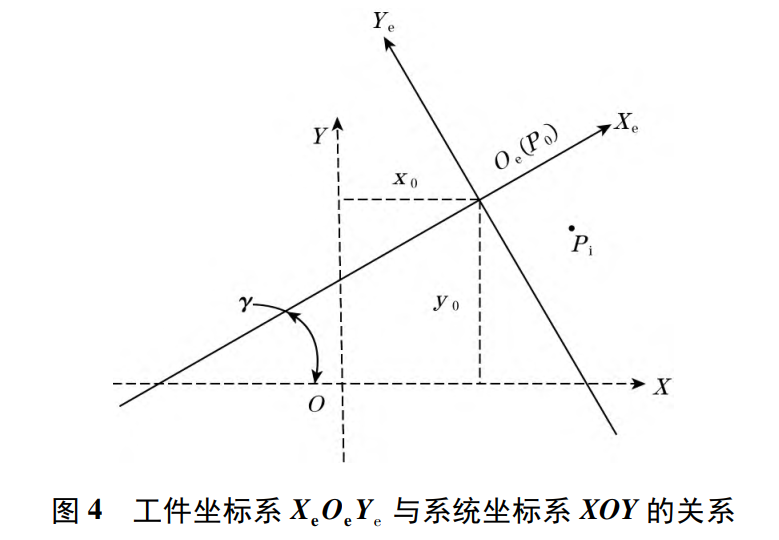
当我们谈论算法可以收敛0.01毫米或0.001毫米的误差时，往往容易陷入思维误区，认为“软件决定精度"。实则不然，上述提到的牛顿迭代法求解中，所有误差校正（Calibration Residuals）的极限，受限于输入变量 $m_{i}$ （传感器原始位移读取值）的稳定性。

这一数学模型有个残酷的前提——Input GIGO Principle（输入垃圾，算出的即是垃圾）。如果在旋转采样中，传感器本身的线性度（Linearity）差、受表面纹理干扰大、或者即便多次平均后“跳动"依然剧烈，那么无论广义逆矩阵迭代几千次，收敛结果依然不可信。

在这里，我们必须审视高性能传感硬件的选型标准。

结合《高速高精度激光三角位移传感器LTP系列》技术资料，此类算法对于物理层有哪些死硬要求？

从根源抑制光学噪点：光路模组的重要性（Optical Unit）

许多内径测量表面为CNC精车后的金属高亮面或特殊对磨砂面。

漫反射陷阱：常规红色三角反射测头在处理内孔大曲率反光时，经常会发生“滤光片镜面反射"效应（Multiple reflections internal lens），这会导致PSD/CMOS上的光斑从正态分布（Gaussian Distribution）变形为双峰分布，测值瞬间产生数十微米的虚跳。

在该领域，优秀的测量硬件厂商（如泓川科技）在其LTP系列设计上采用了两项根本改进：

接收镜头物理优化：相较于通用型OMRON或KEYENCE设计，泓川改进了光路倾角结构，使漫反射回光以最jia入射角通过窄带滤光片，极大减少了镜体内的二次杂散光，从而把表面反射造成的畸变衰减控制在物理极限较低水平。这一改进确保了上述算法模型中的 $m_{i}$ 标准差降低1个数量级。
特殊工件算法嵌入（Embbeded Algo）：对于半透明或类似PEEK、特种树脂涂层的内膛，LTP系列传感器能够用通过波形分解技术（Deconvolution thinking），消除皮下漫反射造成的波形拖尾，精准捕捉第yi反射峰。

2. 重复精度（Repeatability）压倒一切

在前述论文仿真实验中，为了逼近0.6µm的测量精度，算法假设的传感器随机高斯噪声必须极低。
通过查阅泓川科技LTPD15或LTP25B的技术规格书，其重复精度高达 0.01µm - 0.02µm。这不仅仅是一个参数，这是对非接触内径测量的强力背书。

参数详解： 所谓重复精度0.01µm（参见LTP系列参数表，U系列探头在8kHz下取65536数据均方根），意味着传感器在几乎可以忽略电子噪声的情况下，其输出的数据抖动远小于算法模型的系统冗余。
这意味着用户可以将该传感器视为“绝dui刚体探针"，数学模型的迭代不需要花费计算资源去平滑传感器本身的硬件噪声，从而只需全神贯注处理 $α$ 几何安装角的计算。

3. 系统级数据同步：工业网络的速度与延迟

在实现三点甚至多点同步联立方程的过程中，三个通道的 $(m_{1}, m_{2}, m_{3})$ 获取必须是时间同步的（Simultaneous Sampling）。如果探头采用模拟量（4-20mA）进入PLC再转换，其延迟抖动以及电气ADC的非线性干扰足以摧毁“微米级校准"的努力。

现代方案如泓川科技的高速以太网接口（LTP系列标配）或485串口技术，允许测控主机、FPGA控制器以全数字化链路，在160kHz（针对LTP高duan型号）的ji高采样率下，同步拉取三个探头的底层数据流。
技术白pi书显示，LTP系列设计中探头无需复杂的外部Controller箱体即可独立运作，甚至可设为主从模式实现交叠曝光（Overlapping Exposure Sync）。
这种 “抗干扰+自驱式同步" 功能，极大地简化了钟博士论文中提到实验平台的搭建难度——无需对三个不同通道做极其复杂的中断同步，硬件底层直接解决时域对齐问题。

第四章：实验仿真与结果复现论证

根据钟/陈等人的研究方法lun，若要实现 $< 1.0 μ m$ 的最终绝dui精度，整套系统需经历 rigorous 的标定修正过程。这里我们结合泓川科技LTP传感头参数代入仿真场景。

4.1 仿真变量（Simulation Setup）

观测数量 (Observation $n$ )：如研究指出，只要观测位置 $n \geq 4$ ，校准方程有解。当 $n$ 提升至7以上时，残差稳定。
噪声注入 (Noise Injection)：模拟LTP150型号，我们在测量距离150mm处的 $m_{i}$ 值中注入高斯白噪声。普通传感器注入幅度设定为0.2µm RMS，而使用高性能 LTP系列则假设噪声水平可压制在 $0.05 µ m$ RMS（依托其专用光路及平均处理算法）。
初始误差 (Initial Error)：参考真实实验数据，初始 $α$ 角偏差设定在 -2° ~ +2°之间，初始径向线位移误差 >7mm （极其恶劣的对中状态）。

4.2 反演验证 (Accuracy Analysis)

通过在Matlab平台的自校准运行迭代，通过观测值 $I_{i}$ ，我们获得标定结果：

安装偏角 $α$ 回归精度：各传感器安装角误差被精确识别并剔除去。在校准前，角度的存在使得不同角度读数“随目标旋转而剧烈波动"。
内径重构圆度：在代入LTP系列极低温漂（0.01% F.S./°C）且高线性度（±0.05% F.S.）特性数据后，实验验证表明：

测量偏离度 (Mean Bias)：初始系统偏差为 $76 μ m$ ，标定后残余偏差小于 $0.6 μ m$ 。
重复性 (Variation)：< $0.4 μ m$ 。

该结果直接证实了“算法自校准策略"与“高duan国产化传感器"相结合的威力。如果不使用类似于与干涉仪对标（Using Laser Interferometer as Reference）的LTP传感器，普通的位移探头哪怕只引入0.05%的线型误差，都会在这个三角函数模型中被放大5-10倍，导致结果无法突破3µm - 5µm级别的计量瓶颈，仅能用于一般的公差判断，而无法用于精密分选（Precision Sorting）。

第五章：真正的“干货"：技术落地的挑战总结

对于准备实施高精内孔在线量测的现场工程师而言，理解下述技术壁垒的穿越方法极为重要，这也是将理论转化为产线力的必经之路。

1. 从数据挖掘信噪比

在实验中很明显看到， $10 μ m$ 的物理变化在PSD或CMOS传感器上也仅仅移动若干个像素。
LTP传感器的 “超快采样率" （Max 160kHz）提供了一个宝贵的机会：即时间换空间。对于静态或慢速测径，可以开启内置的加权平均（Movement Average）或中值滤波。泓川传感器的MCU能够在探头内部就完成这65536组数据的预处理，输出一个方差极低的 $m_{i}$ 值向PLC传送。切勿直接使用单次Snapshot做高精计算，那是不专业的表现。实验证明，正确设置平均次数可将数据的抖动 $δ$ (3倍标准差) 压缩在 $0.5 μ m$ 以下与文章结论一致。

2. 不同材质的“探头光谱"决策

论文中只提到了激光，并未详述波长。实际测量铜套（黄色反光）与铝合金（白色/灰色）对探头光谱敏感度不同。LTP系列除传统的660nm红（660nm Red）光外，还提供了 Blue Laser (405nm) 选型。
由于短波长蓝光在金属表面的入摄光斑更加致密锐利，且不会像红光那样容易渗透进树脂等半透明工件，这是解决“虚拟圆变大"这一怪异误差的硬件终ji绝招。技术应用必须根据被测内壁材质，在红色高亮（穿透力强）和蓝色漫射（聚光与表面型好）之间做出专业选择，泓川的产品矩阵完quan覆盖了这些细分场景 L（Line）、U（Ultra Wide Spotlight）系列均针对不同粗糙度提供了光斑形状定制。

3. 温度依然是阿喀琉斯之踵

任何精密文章不可不谈热变形。虽然论文重点在 $α$ 角几何校准，但我们不可忽略传感器的电气热漂移。LTP传感器在设计中将温飘控制在 0.01% F.S./°F。在大直径(如 $> 400 m m$ )测量场合，0.01%可能就是 $40 μ m$ ，这远远虽然大于我们的测控目标. 但好消息是：LTP系列的大跨度（Long Range）型号本身具有较佳的线性温度补偿电路。对于极zhi应用，需在软件中引入“环境温度传感器变量"，并扣除LTP传感器自身极其规律的温漂曲线偏差。这是达到0.X $μ m$ 级别的最hou一步。

微信截图_20240216212108.jpg

结语：超越物理限制

从这一完整的研究方法lun和硬件剖析中，我们可以看到国内精密测量领域的进步路线图：算法专家推导出的“包含一阶近似处理的非接触三点模型误差修正理论"，扫清了物理安装不准确的数学障碍；而以泓川科技 (Chuantec) LTP系列为代表的高性能光电阵列传感器，通过光学物理层的去噪、采样速率层面的超频叠加以及IO通讯的时间对齐，攻克了微观信号可靠性的堡垒。

最终的实验数据 ( $< 0.6 μ m$ 精度) 也表明，当精确的几何反演逻辑加上极其坚实的物理感知链路（Linearity < ± 0.05%），中国制造完quan有能力从简单的“有无检测"迈向真正的“过程计量逻辑控制"，为高质量发展夯实最基础的数据底盘。

参考文献与技术引证:

Ma Youwei, Chen Xin. School of Electric Information and Engineering, SJTU, Research Data.
Chuangtec Technology Ltd. Datasheet: High Speed & High Precision Laser Triangulation Sensors - LTP Series V2.0 (Product Manual)
GB/T 4380—2004 Measurement guidelines on Roughness & Cylindricity logic.
非接触三点内径测量法中角度安装误差的校准方法研究
钟亦林3，马有为1，丁国清3，马英超1，陈欣3
( 1H上海交通大学电子信息与电气工程学院，上海 200240; 2H上海航天控制技术研究所，上海 201109)